Początkowe lata nauki szkolnej mają dla dzieci duże znaczenie. To wtedy pojęcia matematyczne są kształtowane propedeutycznie. Wtedy dziecko wyrabia sobie motywującą do działania wiarę we własne możliwości. W tym początkowym okresie nauki kształtują się m.in. umiejętności związane z prowadzeniem różnego typu rozumowań. Z badań wynika, że dzieci chętnie uczestniczą w rozwiązywaniu łamigłówek wymagających sporego wysiłku intelektualnego. Wykazują przy tym dużą dociekliwość poznawczą. Potrafią też skupić się przez dłuższy czas na złożonych zadaniach. Uczący się chętnie samodzielnie wynajdują i rozwiązują zadania ([1], [2]).
Naturalny zapał dzieci może i powinien być wykorzystywany i podtrzymywany u każdego z nich. Każde dziecko jest w stanie osiągnąć sukces i dokonać odkryć matematycznych, oczywiście na miarę swoich możliwości intelektualnych i aktualnie posiadanej wiedzy.
W dalszej części ukażę przykłady zadań – zagadnień do rozważenia z uczniami, w których dla kształtowania kompetencji matematycznych wykorzystuje się naturalną skłonność dziecka do eksperymentowania i zabawy, stwarza się możliwości osiągnięcia sukcesu i czerpania radości z aktywności o charakterze matematycznym. W poszczególnych przykładach mamy do czynienia ze stopniowaniem trudności, dzięki czemu proponowane uczniowi zadania można dostosować do jego kompetencji. Umożliwia to każdemu dziecku działanie na „granicy jego możliwości intelektualnych”, co pozwala na budowanie krok po kroku umiejętności matematycznych.
Przykładowe zadania, dotyczące trójkątów liczbowych, umożliwiają działanie na poziomie czynności konkretnych (dostarczamy uczniowi kartonowy model trójkąta oraz żetony), wyobrażeniowych (uczeń bazuje na trójkątnej planszy z narysowanymi żetonami) lub abstrakcyjnych (uczeń otrzymuje kartkę z narysowanymi trójkątami częściowo uzupełnionymi liczbami).
Praca nad proponowanymi dalej zadaniami umożliwi – w warstwie matematycznej – kształcenie sprawności rachunkowej, w tym umiejętności wyznaczania sumy liczb, rozkładu liczb na składniki, odgadywania liczby (składnika) przy danym składniku i sumie, planowania pracy, opracowywania i realizacji strategii rozwiązania zadania.
Dalej zaprezentowano trójkąty podzielone na części. Obok każdego z boków trójkąta znajdują się prostokątne pola. W każdym z nich znajduje się liczba (lub stosowna liczba żetonów) stanowiąca sumę liczb (żetonów) znajdujących się przy boku danego trójkąta.
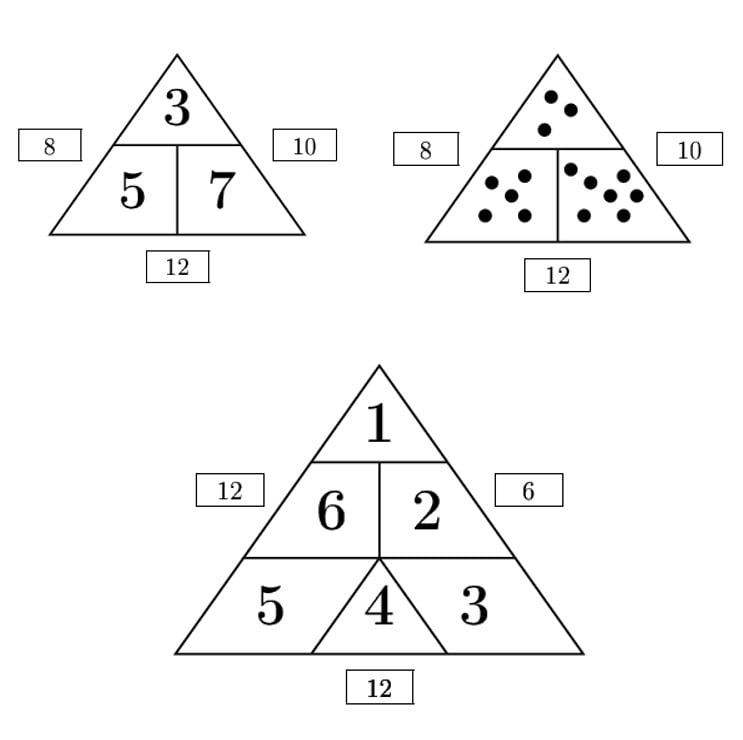
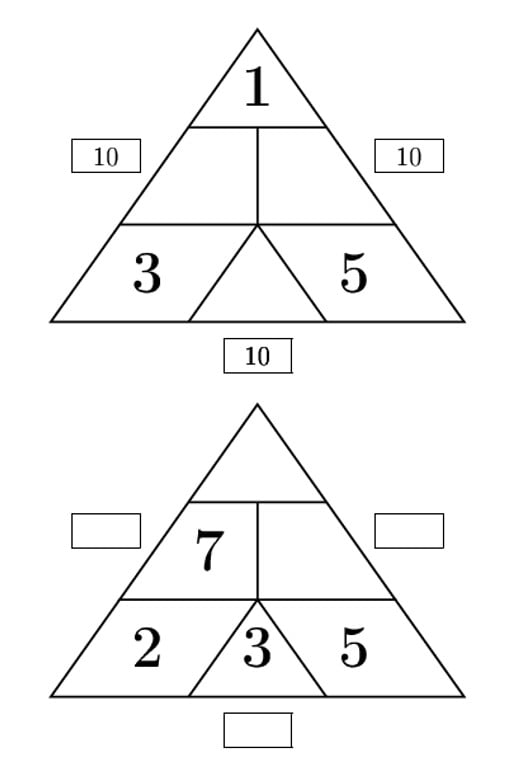
Poniżej znajdują się przykładowe, uzupełnione trójkąty liczbowe.
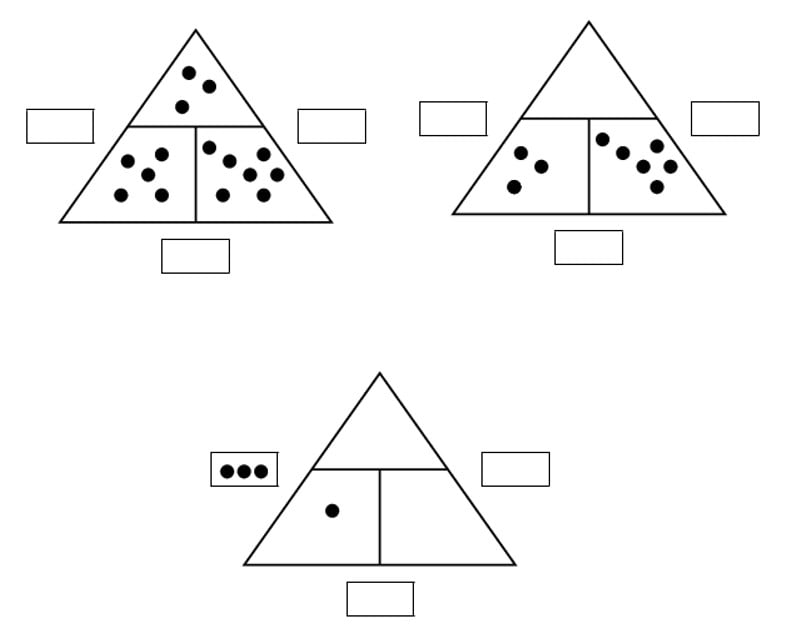
Zadanie 1.
Uzupełnij trójkąty liczbowe układając żetony w pustych sektorach.
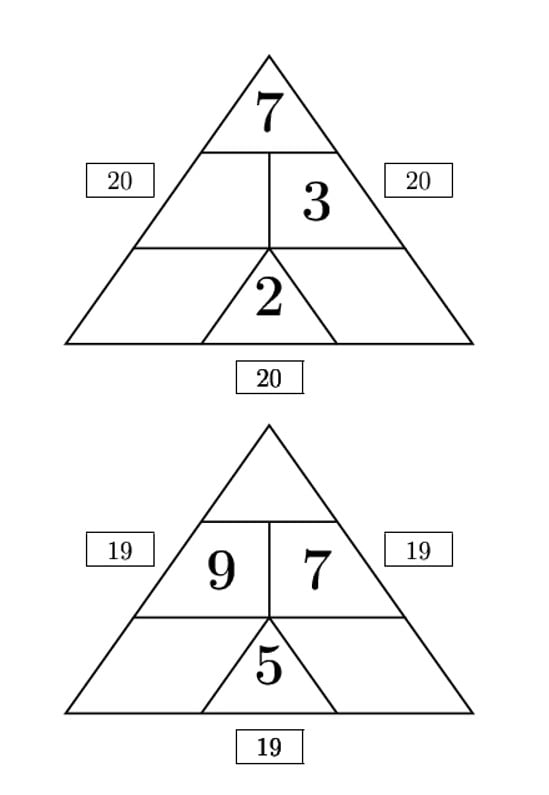
Zadanie 2.
Uzupełnij trójkąty liczbowe wrysowując żetony w puste sektory.
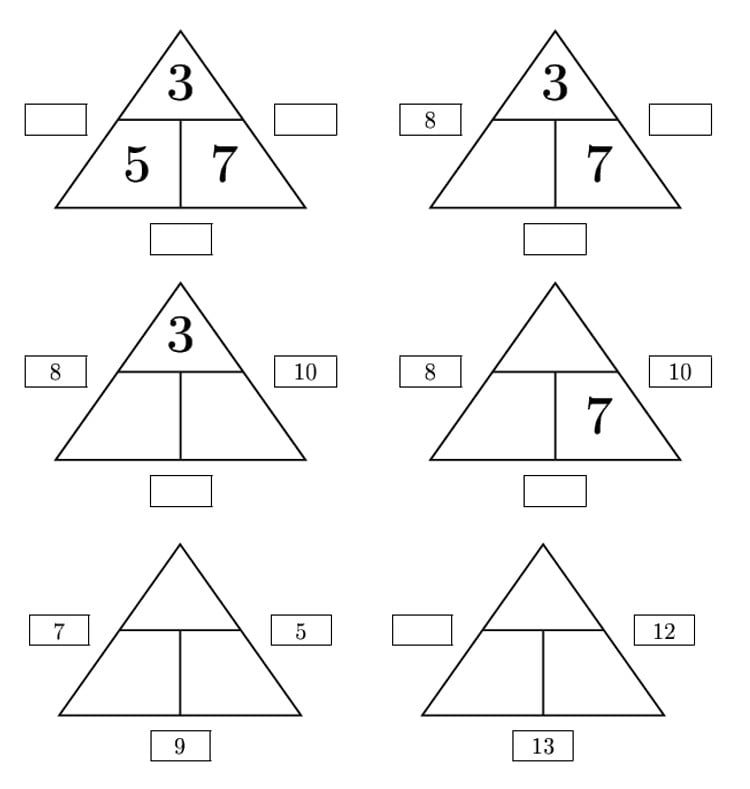
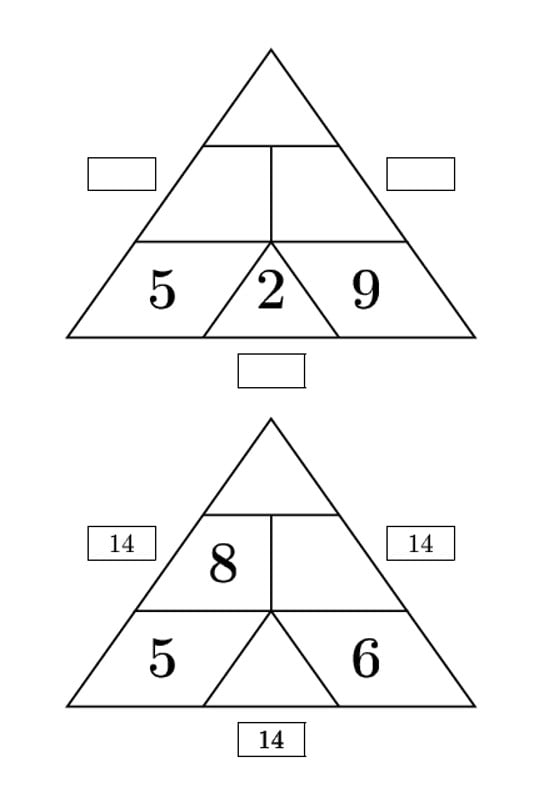
Zadanie 3.
Uzupełnij trójkąty liczbowe wpisując liczby w puste sektory.
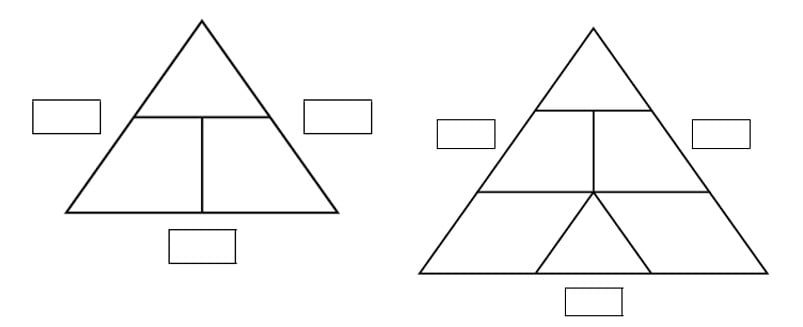
Zadanie 4.
Skonstruuj trójkąt liczbowy układając żetony.
Zadanie 5.
Skonstruuj trójkąt liczbowy wrysowując żetony.
Zadanie 6.
Skonstruuj trójkąt liczbowy wpisując liczby.
Zadanie 7.
Skonstruuj trójkąt liczbowy tak, aby suma liczb przy każdym z boków trójkąta wynosiła 13.
Zadanie 8.
Skonstruuj trójkąt liczbowy tak, aby suma liczb przy każdym z boków trójkąta wynosiła 14, a liczby wewnątrz trójkąta się nie powtarzały.
Podane tu zostały wybrane propozycje różnego typu zadań (dodatkowe trójkąty liczbowe do rozwiązania znajdują się w załączniku). W przypadku zadań z wieloznacznym rozwiązaniem, wartościowym dydaktycznie wydaje się wskazywanie przez uczniów wszystkich możliwości połączone z uzasadnieniem, że więcej możliwości nie ma. W pracy nad niektórymi zadaniami można też stawiać dodatkowe warunki budowy trójkątów, np. liczby wpisane wewnątrz trójkąta nie mogą się powtarzać albo liczby w trójkątach bądź sumy powinny być mniejsze od ustalonej liczby.
Przedstawione zadania umożliwiają uczniom o różnych kompetencjach matematycznych pracę na tym samym materiale. Zauważmy, że gdy dzieci pracują na różnym materiale to w praktyce, w klasie tworzą się grupki osób, które posiadają odmienne od siebie doświadczenia. Taki styl dla uczenia się matematyki niesie wiele ograniczeń. W sytuacji, gdy dzieci pracują na tym samym materiale, aktywność dzieci może być położona na pracę nad zadaniami problemowymi, prowadzącymi do odkrywania nowych dla ucznia faktów, nie zaś na rozwiązywaniu rutynowych zadań – ćwiczeń, jak to ma często miejsce w sytuacji, gdy uczniowie pracują na różnym materiale.
Uczniowie mający podobne doświadczenia mogą współdziałać na poziomie społecznym, mogą wymieniać się doświadczeniami, co niewątpliwie ułatwia uczenie się matematyki i buduje jej społeczny charakter.
Literatura:
[1] Czaplińska J., Nawolska B., Elementy kombinatoryki w nauczaniu dzieci młodszych, Cesty k poznawani v matematyce (sbornik prispevku), Olomouc, 2004, 62-66. [2] E. Gruszczyk-Kolczyńska, Dzieci uzdolnione matematycznie (cz. 1), Psychologia w Szkole, nr 1, 2011 r. [3] J. Nowik, Kształcenie matematyczne w edukacji wczesnoszkolnej, Wydawnictwo Nowik, Opole, 2013.Pobierz materiał z załącznikiem
Autor: dr Joanna Major – dydaktyk matematyki