Autor: dr Maciej Major
Szkoła Podstawowa im. s. Emilii Podoskiej w Grajowie
Od początku edukacji matematycznej do kształcenia włączane są elementy geometrii, arytmetyki i algebry. Natomiast elementy kształcenia probabilistycznego (przez probabilistykę rozumiemy tu fuzję elementów rachunku prawdopodobieństwa, kombinatoryki i statystyki opisowej) występują w Podstawie Programowej na poziomie klas VII-VIII, a tym samym w programach nauczania pojawiają się dopiero pod koniec nauki w szkole podstawowej i to w bardzo ograniczonym zakresie. W obecnej podstawie programowej kształcenia z matematyki dla II etapu edukacyjnego (por. Podstawa Programowa, 2017) elementy statystyki opisowej występują po raz pierwszy w klasach IV-VI. Znajdujemy tu: gromadzenie i porządkowanie danych; odczytywanie i interpretowanie danych przedstawionych w tekstach, tabelach, na diagramach i na wykresach.
Zagadnienia te są rozszerzane w klasach VII-VIII. Znajdujemy tu:
- interpretowanie danych przedstawionych za pomocą tabel, diagramów słupkowych i kołowych, wykresów, w tym także wykresów w układzie współrzędnych;
- tworzenie diagramów słupkowych i kołowych oraz wykresów liniowych na podstawie zebranych przez siebie danych lub danych pochodzących z różnych źródeł;
- obliczanie średniej arytmetycznej kilku liczb.
Elementy kombinatoryki i rachunku prawdopodobieństwa pojawiają się dopiero w klasach VII-VIII. W przypadku kombinatoryki autorzy Podstawy Programowej zwracają uwagę na ,,zaawansowane metody zliczania” mocy różnych zbiorów. Ich zdaniem uczeń powinien:
- stosować regułę mnożenia do zliczania par elementów o określonych własnościach;
- stosować regułę dodawania i mnożenia do zliczania par elementów w sytuacjach wymagających rozważenia kilku przypadków, na przykład w zliczaniu liczb naturalnych trzycyfrowych podzielnych przez 5 i mających trzy różne cyfry (…).
Z kolei z zakresu rachunku prawdopodobieństwa uczeń powinien:
- obliczać prawdopodobieństwa zdarzeń w doświadczeniach, polegających na rzucie dwiema kostkami lub losowaniu dwóch elementów ze zwracaniem;
- obliczać prawdopodobieństwa zdarzeń w doświadczeniach, polegających na losowaniu dwóch elementów bez zwracania (…).
Jednocześnie dydaktycy matematyki zwracają uwagę na konieczność zapoznawania uczniów z elementami probabilistyki możliwie wcześnie (por. Czaplińska, Nawolska, 2004). Zdaniem H. Freudentala ,,…proces rozwijania myślenia probabilistycznego u uczniów powinien odbywać się w sposób systematyczny, równolegle z rozwojem myślenia deterministycznego. Ponadto powinien być kontynuowany w ciągu wielu lat nauki, zatem należy go rozpocząć możliwie wcześnie’’ (por. Łakoma, 1988). Warto zwrócić uwagę na fakt, że H. Freudental w swojej koncepcji nauczania kładł duży nacisk na możliwie wielostronne wprowadzanie uczniów w proces matematyzacji rozumianej jako porządkowanie rzeczywistości odbywające się za pomocą matematycznych środków, zaś rachunek prawdopodobieństwa uważał za jedną z najlepszych dróg urzeczywistnienia tego celu.
W związku z faktem, że zagadnienia kombinatoryczne występują w programach nauczania dopiero w dwu ostatnich klasach szkoły podstawowej podjęto badania dotyczące możliwości wprowadzania elementów stochastyki do nauczania od początku II etapu edukacyjnego. Nie chodzi tu oczywiście o możliwości zapoznawania uczniów z gotowymi elementami teorii z zakresu probabilistyki, ale o możliwości odkrywania pojęć probabilistycznych przez uczniów oraz rozwijanie ich probabilistycznego myślenia i propedeutyczne kształtowanie pojęć stochastycznych. Wydaje się to istotne w procesie kształcenia, m.in. ze względu na fakt, że w otaczającej nas rzeczywistości występuje wiele zjawisk losowych.
Badania, których fragment tu omówimy, dotyczące myślenia kombinatorycznego uczniów, prowadzone były w II semestrze roku szkolnego w podkrakowskiej szkole podstawowej. Zostały przeprowadzone w dwu etapach. W pierwszym etapie uczniowie pracowali nad kwestionariuszem badań. Etap drugi badań to rozmowa z uczniami na temat rozwiązań zadań. Badania prowadzono w małej (10 osobowej) grupie uczniów klasy IV o zróżnicowanych umiejętnościach matematycznych.
Celem badań była m.in. próba uzyskania odpowiedzi na pytanie, czy uczniowie klasy IV są w stanie, bazując na swoich umiejętnościach i wiedzy, uzyskać rozwiązania zadań kombinatorycznych.
W toku badań zaproponowano uczniom do rozwiązania kilka zadań. Wśród nich znalazły się zadania dotyczące kombinacji (2-elementowych ze zbioru 4-elementowego oraz 3- elementowych ze zbioru 4-elementowego) i permutacji (3 oraz 4-wyrazowych).
Ze względu na nieznajomość przez uczniów terminów kombinatorycznych zadania – pytania sformułowano następująco:
- Z1. Na ile sposobów możesz zaprosić na przyjęcie 2 spośród 4 osób?
- Z2. Na ile sposobów możesz zaprosić na przyjęcie 3 spośród 4 osób?
- Z3. Na ile sposobów możesz załadować na 3 wagony 3 różnokolorowe klocki (żółty, zielony, niebieski), tak aby w każdym wagonie znajdował się dokładnie jeden klocek? Wypisz lub narysuj wszystkie rozwiązania.
- Z4. Na ile sposobów możesz załadować na 4 wagony 4 różnokolorowe klocki (żółty, zielony, niebieski, różowy), tak aby w każdym wagonie znajdował się dokładnie jeden klocek? Wypisz lub narysuj wszystkie rozwiązania.
- Z5. Ile różnych liczb 3 cyfrowych można utworzyć z cyfr 1, 2, 3? Wypisz lub narysuj wszystkie rozwiązania.
- Z6. Ile różnych liczb 4 cyfrowych można utworzyć z cyfr 1, 2, 3, 4? Wypisz lub narysuj wszystkie rozwiązania.
Uczniowie odpowiadając na pytania mieli pełną swobodę co do metody zaprezentowania swoich rozwiązań. Dzięki temu możliwym było obserwowanie w jaki sposób uczniowie matematyzowali sytuacje opisane w treściach zadań.
Uczniowie odpowiadając na pytanie Z1 najczęściej wypisywali wszystkie możliwości. Przy tym większość uczniów nadała poszczególnym czterem osobom, o których mowa w treści zadania, imiona bądź oznaczała poszczególne osoby różnymi kolorami i w rozwiązaniu rysowała – pogrupowane po dwie – różnokolorowe kreski.
Prawie wszyscy uczniowie przedstawiali tu rozwiązania mające podobną strukturę do rozwiązania zaprezentowanego na Rysunku 1.

Po wypisaniu wszystkich możliwości uczniowie podawali odpowiedź. Jest 6 możliwości.
Warto również wspomnieć o jednej pracy, której autorka ,,na siłę” próbuje zapisać treść zadania z użyciem symbolu literowego. Próbuje ułożyć działanie do zadania. Manipuluje przy tym liczbami występującymi w treści (zob. rysunek 2).
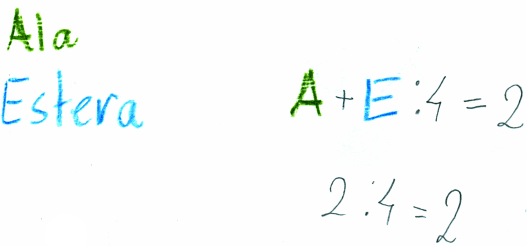
Autorka zapisuje wyrażenie, następnie zakłada, iż A = E = 1. Wyciąga stąd wniosek, że prawidłową odpowiedzią na pytanie postawione w treści zadania jest 2.
Podczas rozwiązywania zadania Z2 większość osób obrała identyczną jak dla zadania Z1 metodę rozwiązania. Rysunek 3 prezentuje przykładowe prawidłowe rozwiązanie zadania Z2.
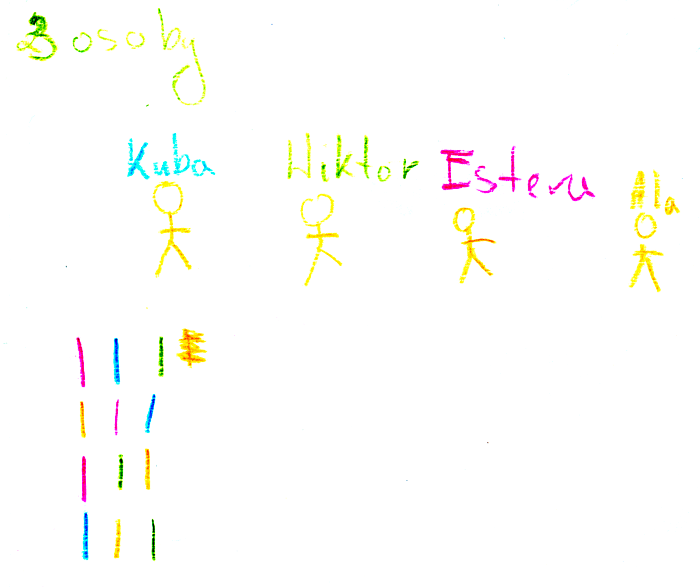
Warto nadmienić, że w trakcie rozmowy podsumowującej różne rozwiązania zadania Z2, jedna z uczennic zwróciła uwagę, że rozwiązania muszą być 4. Stwierdziła: zapraszając 3 spośród 4 osób nie zapraszamy jednej osoby, a jedną osobę wybieramy na 4 sposoby.
Odpowiadając na pytanie z zadania Z3 większość uczniów uzyskała poprawną odpowiedź (6 możliwości). Uczniowie przy tym wyrysowywali wszystkie możliwości (por. rysunek 4).

Trzy osoby nie uzyskały poprawnego rozwiązania. Dwie z nich zilustrowały jedynie dane zadania za pomocą rysunku (por. rys. 5).

Trzecia osoba podała (narysowała) tylko 3 możliwości. Istota tego rozwiązania bazuje na niezawartym w treści zadania fakcie, że klocek w danym kolorze w danym wagonie może pojawić się tylko raz (por. rys. 6).

Uczniowie odpowiadając na pytanie zawarte w zadaniu Z4 stosowali analogiczną metodę rozwiązania do metody stosowanej przy rozwiązywaniu zadania Z3. Niestety, tylko jedna osoba podała poprawną odpowiedź. Osoba ta rozpoczęła wyrysowywanie wszystkich możliwości (narysowała wszystkie pociągi z klockiem różowym w pierwszym wagonie – 6 pociągów), a następnie zapisała, że liczba pociągów będzie 4-krotnie większa, tj. będzie ich 24.
Pozostali uczniowie popełnili w rozwiązaniach błędy polegające w głównej mierze na pominięciu pewnych możliwości (permutacji). Wynikało to najprawdopodobniej z tego, że wszystkich pociągów jest aż 24, a więc wyznaczanie (wskazanie) ich wymaga pewnej systematyczności, której częściowo rozwiązującym zabrakło. Dla ilustracji prezentujemy dwa wybrane rozwiązania (zob. rys. 7 i rys 8).


Warstwy matematyczne zadań Z5 i Z3, a także zadań Z6 i Z4 są identyczne, więc i odpowiedzi liczbowe są takie same. Pary zadań różni warstwa treści, przy czym zadania Z5 i Z6 są zadaniami czysto matematycznymi. Uczniowie nie dostrzegli analogi pomiędzy parami zadań, każde z nich rozwiązywano niezależnie. Przy czym dużo większe trudności stwarzało uczniom rozwiązanie zadań Z5 i Z6. Być może przyczyną tego jest fakt, że rozwiązując zadania matematyczne uczniowie próbują zastosować znane im algorytmy i schematy postępowania, zaś podczas rozwiązywania zadań Z3 i Z4 poszukują rozwiązań, kierując się własnym doświadczeniem i zdrowym rozsądkiem.
Warto zwrócić uwagę na fakt, że wypisywanie przez uczniów wszystkich możliwości było bardziej systematyczne w przypadku zadań z kontekstem realistycznym, niż w przypadku zadań o liczbach.
W zadaniu Z6 tylko jedna osoba podała poprawne rozwiązanie. Jej rozumowanie było analogiczne do rozumowania prowadzonego przez nią w rozwiązaniu Z4 (por. rysunek 9).

Wśród badanych znalazła się jedna osoba, która odpowiedzi liczbowe do wielu zadań podawała na podstawie szacowania, a można przypuszczać, że i zgadywania liczby możliwości.
W rozmowie prowadzonej z uczniami badani stwierdzili, że zaproponowane zadania są interesujące i odmienne od tych, które na co dzień rozwiązywane są na lekcjach matematyki. Uczniowie zwracali też uwagę, że zagadnienia o których mowa w zadaniach występują w życiu codziennym. Warto tu podkreślić, że uczniowie pracowali nad zadaniami bardzo chętnie.
Obserwacje poczynione podczas prowadzonych badań, pozwalają stwierdzić, że pewne treści probabilistyczne mogą być wprowadzane już na progu II etapu edukacyjnego. Dzięki odpowiedniemu sformułowaniu zadań możliwym jest rozwijanie u uczniów umiejętności kodowania informacji. Proponowanie uczniom zadań podobnych do opisanych powyżej pozwala też kształtować elementarne intuicje probabilistyczne, a także systematyczność w wypisywaniu wszystkich rozwiązań. Pozwala więc też kształtować logiczne, strukturalne myślenie.
W dalszej części prezentuję przykładowy (odmienny od przytoczonego wyżej) zestaw zadań, który można proponować uczniom w ,,młodszych” klasach szkoły podstawowej. W warstwie matematycznej zadania dotyczą kombinacji 2-, 3- i 4-elementowych.
Z1. Pan Józef sprzedaje lody w 3 smakach: czekoladowe, śmietankowe, pomarańczowe. Ania chce kupić 2 kulki lodów w różnych smakach. Narysuj jak najwięcej rożnych zestawów lodów jakie może kupić Ania. Lody czekoladowe zaznacz na brązowo, śmietankowe na biało, a pomarańczowe na pomarańczowo.
Z2. Pan Józef sprzedaje lody w 4 smakach: czekoladowe, śmietankowe, pomarańczowe i truskawkowe. Ania chce kupić 3 kulki lodów w różnych smakach. Narysuj jak najwięcej rożnych zestawów lodów jakie może kupić Ania. Lody czekoladowe zaznacz na brązowo, śmietankowe na biało, pomarańczowe na pomarańczowo, a truskawkowe na czerwono.
Z3. W kawiarni sprzedawane są lody w pucharkach po 2 gałki w rożnych smakach. Dostępne są lody czekoladowe (w kolorze brązowym), śmietankowe (w kolorze białym), truskawkowe (w kolorze czerwonym), pomarańczowe (w kolorze pomarańczowym). Narysuj jak najwięcej różnych zestawów lodów jakie można kupić w kawiarni.
Rozwiązywanie zadań Z1-Z3 można poprzedzić wykonywaniem ćwiczeń manipulacyjnych. Uczniowie mogą układać (nad rysunkami lodowych rożków) różnokolorowe koła symbolizujące lody w poszczególnych smakach.
Literatura:
- Czaplińska J, Nawolska B, Elementy kombinatoryki w nauczaniu dzieci młodszych, Cesty (k) poznávání v matematice primární školy, Olomouc, Univerzita Palackého, 2004.
- Łakoma E. O poglądach H. Freudentala na temat nauczania rachunku prawdopodobieństwa i statystyki, Matematyka 4, 1988, 204-213.
- Łakoma E., H. Freudental o kształtowaniu podstawowych pojęć probabilistycznych, Matematyka 2, 1989, 82-90.
- Major M., B. Nawolska, Matematyzacja, rachunki, dedukcja i interpretacja w zadaniach stochastycznych, Wydawnictwo Naukowe WSP, Kraków 1991.
- Podstawa Programowa kształcenia ogólnego dla szkoły podstawowej. Dz.U. 2017, poz. 356, 2017.


